How to Solve questions related to Mensuration: Tricks and Practice Questions

In CLAT, to score good marks in Quantitative Aptitude, one should have good Command over elementary Mensuration. In Mensuration, you should have some basic knowledge of Area & Volume of Rectangle, Square, Parallelogram, rhombus, Cube, Cuboid, Cylinder, Sphere, Cone.

How to Solve questions related to Mensuration: Tricks and Practice Questions

Formulas related to Mensuration

A. Cuboid

 

 

 

 

 

l: length b:breadth h:height

Lateral surface area (LSA) = 2h(l+b)

Total surface area (TSA)= 2 (lb +bh+hl

Volume=LxBxH

B. Cube

 

 

 

 

 

 

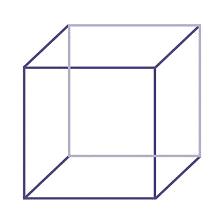
a: Edge of the cube

Lateral surface area (LSA) =4a²

Total surface area (TSA)=6a²

Volume=a³

C. Cylinder

 

 

 

 

 

 

 

 

 

h: height r: radius

Lateral surface area (LSA) = 2πrh

Total surface area (TSA)= 2πrh+2πr²

Volume=πr²h

D. Cone

 

 

 

 

 

 

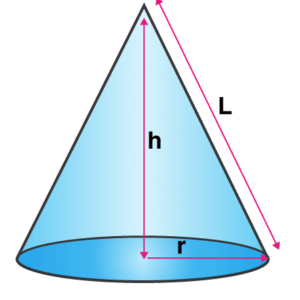
l: slant height r: radius h: height

Lateral surface area (LSA) = πrl

Total surface area (TSA)= πrl+πr²

Volume=1/3πr²h

E. Sphere

 

 

 

 

 

 

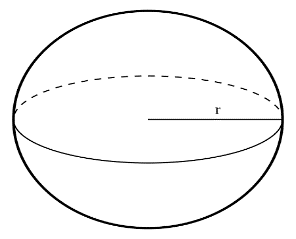
h: height r: radius

Lateral surface area (LSA) = 4πr²

Total surface area (TSA)= 4πr²

Volume=4/3πr³

F. Hemisphere

 

 

 

 

 

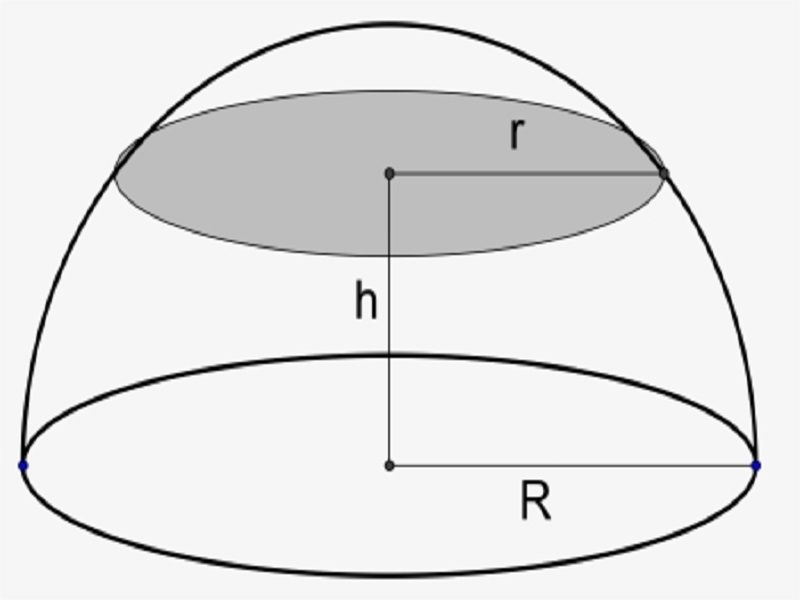
h: height r: radius

Lateral surface area (LSA) = 2πr²

Total surface area (TSA)= 3πr²

Volume=2/3π³

Tips to solve Mensuration based questions

1. Try to learn square and cube of 1 to 30, it will help you to avoid extra calculations and save time.
2. Try to learn all formulas of mensuration on tips, as by using formulas you can avoid calculations.
3. In question, if the values are given in decimal then use pie value as 3.14, if the values are in fraction then use pie value as 22/7.
4. In mensuration it is not essential to find all the values to get to an answer, always check that which area is mentioned to find. For example, if in a question there is a cone made in the square and a question is asked to you regarding the volume of the cone, then you should find only the volume of the cone not the volume of the square.
5. To solve questions quickly, as most of the students just read the questions and start to solve them, but they should also analyze the diagram of the questions properly.
6. In mensuration to find the volume of a combination of two or more basic solids, we should add their volumes.
7. In mensuration to find the surface areas of a combination of two or more solids, it is not necessary to add their surfaces directly.

Sample question

A room having the dimensions as mentioned in the chart below has a table, a bed, and a chair. There are three books kept on the table (side by side) and also a lamp having a radius, 3.5 inches. Now, based on the information given below answer the following?

S.No	Object	Length	Breadth	Height
1	Room	18	12	12
2	Bed	3.5	6	3
3	Table	3	4	4
4	Chair	2	2.5	4
5	Books	12	6	3

1. What would be the area of the room that is not covered by any object as mentioned above?

1. 176.5 sq. ft
2. 178 sq. ft
3. 367 sq. ft
4. 245.5 sq. ft.

Answer: (b)

2. What is the area of the table which is uncovered by any of the objects?

1. 1656 sq. inch
2. 52 sq. inch
3. 52 sq. inch
4. 1512 sq. inch.

Answer: (c)

3. How many tables are required to cover the floor surface of the room completely?

1. 18
2. 11
3. 21
4. Data are inadequate.

Answer: (a)

4. If the entire room is to be filled with books having the same dimensions as lying on the table then how many books are required.

1. 2,00,736
2. 20,736
3. 11,736
4. 17,522.

Answer: (b)

5. How many chairs can be put inside the room to cover the entire floor area of the room?

1. 40
2. 21
3. 43
4. 18.

Answer: (c)

SOURCE: CLAT 2020 EXAM QUESTION PAPER

---

1. Law Library: Notes and Study Material for LLB, LLM, Judiciary and Entrance Exams
2. Legal Bites Academy – Ultimate Test Prep Destination